Um inteiro (pronuncia-se IN-tuh-jer) é um número inteiro (não um número fracionário) que pode ser positivo, negativo ou zero.
Exemplos de números inteiros são: -5, 1, 5, 8, 97, e 3.043,
Exemplos de números que não são números inteiros são: -1.43, 1 3/4, 3.14, .09, e 5.643.1.
O conjunto de inteiros, denotado Z, é formalmente definido da seguinte forma:
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Em equações matemáticas, inteiros desconhecidos ou não especificados são representados por letras minúsculas, em itálico, a partir do "meio tardio" do alfabeto. As mais comuns são p, q, r, e s.
O conjunto Z é um conjunto denumerável. Denumerabilidade refere-se ao fato de que, embora possa haver um número infinito de elementos em um conjunto, esses elementos podem ser denotados por uma lista que implica a identidade de cada elemento do conjunto. Por exemplo, é intuitivo da lista {..., -3, -2, -1, 0, 1, 2, 3, ...} que 356.804.251 e -67.332 são inteiros, mas 356.804.251,5, -67.332,89, -4/3, e 0,232323 ...não são.
Os elementos de Z podem ser emparelhados um-a-um com os elementos de N, o conjunto de números naturais, sem que nenhum elemento seja deixado de fora de nenhum dos dois conjuntos. Let N = {1, 2, 3, ...}. Então o emparelhamento pode proceder desta forma:
<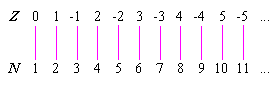
Em conjuntos infinitos, a existência de uma correspondência um-para-um é o teste decisivo para determinar a cardinalidade, ou tamanho. O conjunto de números naturais e o conjunto de números racionais têm a mesma cardinalidade que Z. Entretanto, o conjunto de números reais, números imaginários e números complexos tem uma cardinalidade maior que a de Z.
.
