Um número racional é um número determinado pela razão de algum número inteiro p para algum número natural não nulo q. O conjunto de números racionais é denotado Q, e representa o conjunto de todas as razões possíveis de números inteiros para números naturais p/q.Em expressões matemáticas, números racionais desconhecidos ou não especificados são representados por letras minúsculas, em itálico, do meio ou fim do alfabeto, especialmente r, s, e t, e ocasionalmente u até z. Números racionais são principalmente de interesse para os teóricos.A matemática teórica tem aplicações potencialmente abrangentes em comunicações e informática, especialmente em criptografia de dados e segurança.r e t são números racionais tais que r < t, então existe um número racional s tal que r < s < t. Isto é verdade, não importa quão pequena seja a diferença entre r e t, desde que os dois não sejam iguais.Denumerabilidade refere-se ao fato de que, mesmo que um conjunto possa conter um número infinito de elementos, e mesmo que esses elementos possam estar "densamente embalados", os elementos podem ser definidos por uma lista que atribui a cada um deles um número único numa seqüência correspondente ao conjunto de números naturais N = {1, 2, 3, ...}..
Para o conjunto de números naturais N e o conjunto de inteiros Z, nenhum dos quais é "denso", as listas de desumeração são simples.Para Q, é menos óbvio como tal lista pode ser construída. Um exemplo aparece abaixo. A matriz inclui todos os números possíveis da forma p/q, onde p é um número inteiro e q é um número natural não nulo.Seguindo a linha rosa, pense em 0 como a "primeira parada", 1/1 como a "segunda parada", -1/1 como a "terceira parada", 1/2 como a "quarta parada", etc. Isto define uma lista sequencial (embora redundante) dos números racionais. Existe uma correspondência um-para-um entre os elementos da matriz e o conjunto de números naturais < forte>N.
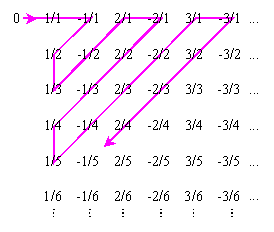
Para demonstrar uma verdadeira correspondência um-para-um entre Q e N, uma modificação deve ser adicionada ao algoritmo mostrado na ilustração.Por exemplo, 2/4 = 3/6 = 4/8 = 5/10, etc. Estas redundâncias podem ser eliminadas através da imposição da restrição: "Se um número representa um valor previamente encontrado, pule sobre ele."Desta forma, pode ser rigorosamente provado que o conjunto Q tem exatamente o mesmo número de elementos que o conjunto N.Algumas pessoas acham isso difícil de acreditar, mas a lógica é sadia.
Em contraste com os números naturais, inteiros e racionais, os conjuntos de números irracionais, números reais, números imaginários e números complexos são não-denumeráveis. Eles têm uma cardinalidade maior que a do conjunto N.Isto leva à conclusão de que alguns "infinitos" são maiores que outros!
